「○○が××を引き起こした」

 日常会話では、「○○のせいで××になった」とか、「○○が××の原因だ」とか、「○○が××を引き起こした」といった発言を、私たちはかなり気軽に行っています。
 上の鍵括弧内のような発言は、因果関係を主張しているものです。○○という原因があったから、××という結果が起きたのだ、という関係ですね。

 しかし、もしもわずかなりともアカデミックな、あるいは厳密な議論を要する場にいるならば、因果関係という語には極めて慎重にならなければなりません。
 さもなくば、あなたのもとに「ドーモ、トウケイ・ガクシャです。素人質問で恐縮なのですが……」とニンジャがエントリーしてくることになるでしょう。コワイ！
 そんな恐ろしいニンジャを避けるために、今回は因果関係の話をしましょう。
 ……なお、申し訳程度の歴史要素として、後半には「大恐慌後の金本位制の離脱は、実質金利を低下させたのか？」という問題の因果推論の論文を扱います。

あなたはヨーグルト会社の社長です

 まずは、因果関係を主張することがどれだけ難しいか、という話を、具体例を使って考えてみます。
 あなたはヨーグルト会社の社長だとしましょう。そこへ、経済学を修めたと称する怪しげなコンサルがやってきてこう言います。
「うちの製品を使いましょう！　そうすれば売り上げが倍になります！」
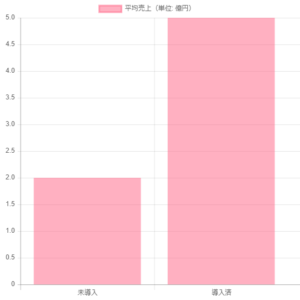（グラフ作成には「ちゃちゃっと」: https://chachart.net/bar を使用）

 そのコンサルは続けて、
「このグラフを見てください！　弊社製品を導入している企業は、そうでない企業の倍以上を売り上げています！　弊社製品が売り上げを大きく増やしたんです！　だから、御社も弊社製品を導入すれば売り上げが増えますよ！」
などとのたまうわけです。
 さぁ、ヨーグルト会社の社長たるあなたはどうしますか？

 正解は……
「イヤーッ！」
「グワーッ！　サヨナラ！」コンサルは爆発四散！
 アイサツ前のアンブッシュは一度まで認められています。アンブッシュにも耐えられないコンサルは実際サンシタなため、話を聞く必要もない。

 あっはい。真面目にやります。
 さて、先ほどのグラフをもう一度見てみてください。このグラフは、製品の導入と売上に相関があることを示しています。
 では、その相関関係が因果関係であると、つまり、製品を導入した「から」売上が増えた、という関係があると言えるでしょうか？

 私がそのヨーグルト会社の社長だったら、迷いなくコンサルにアンブッシュを仕掛けます。じゃないや、ええと、製品を導入した「から」売り上げが増えた、とは言えないと思います。
 考えられる他の理由は、大きく3種類に分けられます。

 まず1つ目が、まったくの偶然という可能性です。
 有名な例としては、ニコラス・ケイジと何かを結び付けるやつですね。ニコラス・ケイジの映画出演数とプールの溺死者数とか。
 ここでは、ニコラス・ケイジの映画出演数と、ノースダコタ州の運輸保安検査官の数の相関を貼っておきます。綺麗に相関しているように見えますが、これを因果関係だと主張するのは相当難しいでしょう。
 ニコラス・ケイジが出演する→身体は闘争を求める→犯罪リスクが高まる→保安検査官が増える……なんて、さすがに無理筋。その次はアーマードコアの新作でも出るのか？

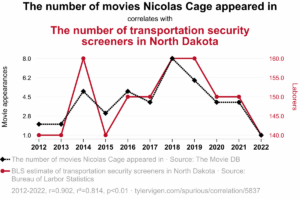
（出典: Tyler Vigen – Spurious Correlations: https://tylervigen.com/spurious/correlation/5837）

 とはいえ、このコンサルの例では（導入済企業数がとんでもなく少ないとかでない限りは）完全な偶然とは言いにくいでしょう。命拾いしたな。

 では第2の理由、逆向きの因果がある可能性に行ってみましょう。つまり、製品を導入したから売上が増えた、のではなく、売上が高いから製品を導入した、ということです。
 これは可能性がありそうです。売上の少ない企業は、そもそも製品を導入する余裕なんかないんじゃないかと言われれば、コンサルも「アバーッ！」と爆発四散することでしょう。

 最後の理由は、まったく別の、第3の要因が関係している可能性です。
 色々と考える余地があるのですが、たとえば、コンサルが大企業にばかり営業をかけているとしてみましょう。この場合、大企業であることが、営業→導入の要因であると同時に、売上の大きさの要因でもあります。
 この場合も、製品導入が売上を増やしたという因果関係があるとは言えませんね。コンサルはしめやかに爆発四散！

 これで、「因果関係」を主張することの難しさについてはご理解いただけたと思います。反対に、もしもあなたがコンサル側の立場なら、こうした指摘にも耐えられるように理論武装重点で挑む必要があるということです。備えよう。

 ところで、さらに追い打ちをしておくと、たとえ、製品を導入したから売上が増えたという因果関係があったとしても、ヨーグルト会社がこれを導入すべきかは断言できません。なぜなら、そのヨーグルト会社にとって、売上が増えるかどうかは定かではないからです。
 これはいわゆる「外的妥当性」という問題です。たとえば、売上が増えた企業たちは、ヨーグルトとはまったく違うものを作っている企業かもしれません。ブロッコリーとか。そのときには、ヨーグルト会社にもそのまま同じ結果が現れるとは考えにくいでしょう。

Rubinの因果モデル

 それでは、厳密な因果関係を立証するためにはどうすればいいのでしょうか？
 勘のいい方はお気づきかもしれませんが、「厳密な」議論をするためには、数学を避けて通ることはできません。ここでは、ちょっとだけ数学を使って、因果関係を考えてみましょう。
 なお、どうしても数学が苦手だという方は、ここは読み飛ばしてもらっても構いません。

 いま、iさんの原因となる処置をDᵢとしましょう。DᵢはYes（Dᵢ=1）かNo（Dᵢ=0）のいずれかになるような変数です。一方で、原因が決まったのちのiさんの結果（潜在アウトカム）はYᵢ(1), Yᵢ(0)として、Yᵢ(1)もYᵢ(0)も実数値を取るとしましょう。
 先ほどの例でいえば、Dᵢはi社の製品の導入（Dᵢ=1）と非導入（Dᵢ=0）に対応し、Yᵢ(1)は導入したときのi社の売上、Yᵢ(0)は導入しなかったときのi社の売上です。

 こういうふうに書いたとき、Dの処置効果（Treatment Effect: TE）は、以下のように定義できます。

TE=Yᵢ(1)-Yᵢ(0)

 これが正なら、i社にとって、製品の導入（D=1）は売上Yを増やすという因果関係がある、と明確に言うことができるわけです。この程度はチャメシ・インシデント。

 ……ということで終わるのならよかったのですが、残念ながら、そうもいきません。
 なにせ、Yᵢ(1)とYᵢ(0)というのは同時に観測することはできないのです。i社が製品を導入した（D=1）場合、「製品を導入しなかったときのi社の売上」であるYᵢ(0)は反実仮想であって、現れるわけがありません。その逆も然りです。
 ですから、もしあなたが科学力の乏しい場所にいて、平行世界を観察する機械も、タイムマシンも持っていないのだとすれば、残念ながらこの方法は諦めるしかないのです。

 そんな中で、可能な方法は期待値（平均）を取ることです。平均処置効果（Average Treatment Effect: ATE）は期待値をEとして、以下のように定義できます。

ATE=E[Yᵢ(1)-Yᵢ(0)]

 これが正なら、Dという処置（製品の導入など）は、「平均的には」Y（売上など）を増やすという因果関係がある、と言えます
 詳細な計算は省きますが、もしも、処置を受けていた人（Dᵢ=1）と、受けていなかった人（Dᵢ=0）の間で、「処置を受けなかったときの期待値」と「処置を受けたときの期待値」がそれぞれ同じ（E[Yᵢ(1)|Dᵢ=1]=E[Yᵢ(1)|Dᵢ=0], E[Yᵢ(0)|Dᵢ=1]=E[Yᵢ(0)|Dᵢ=0]）だと信じるに足る根拠があるのならば、このATEを求めることができます。
 具体的には、ランダム化比較試験（Randomized Controlled Trial: RCT）を行った場合が対応します。くじ引きか何かで、まったくのランダムに処置を受けるか受けないかを決めた場合には、上述したような仮定が成り立つと考えることができます。

 しかし、こと歴史学や経済学の領域では、こうした実験も困難なことが多いのです。
 「くじ引きで当たったので、うちの製品導入してください」くらいはまだ何とかなるかもしれませんが、「くじ引きで当たったので、1930年に金本位制離脱していたことにしてください」なんてタイムマシンがないとできない（あってもたぶんできない）わけでして。
 さらに、しばしば倫理的問題も関係します。有名なAngrist (1990) は「従軍経験があると所得が低くなる」という問題を研究しましたが、これをRCTでやったら、「くじ引きで当たったので、戦争に行って来てください」ということになってしまうわけです。おお、ブッダよ、寝ているのですか！
 もちろん、そんなくじ引きで従軍させるなんて無法がまかり通るわけがありません。実際、Angrist (1990）は「自然実験」という、たまたま実験のような状況が生まれたケースを上手く活用して因果関係を示しました。詳細が知りたい方は、2年前くらいに私もちょろっと動画を作ったので、ご参考までに。

 さて、実験もできない、自然実験も見当たらないとなったら、後は相当手の込んだ方法をやるしかありません。
 ここでは、その中でもまだ単純なものとして、差の差の分析（Difference in Difference: DiD）を扱いましょう。

事例: 金本位制離脱は実質金利を低下させたのか？

 1929年の大恐慌後、世界各国は相次いで金本位制を離脱しました。その結果、インフレ期待が高まり、実質金利が低下し、景気回復につながった、というストーリーには、おおかたの経済史研究者が同意するところでしょう。
 しかし、この因果関係をデータを用いて実証しようとするならば、かなりの困難が伴います。もちろん、実験なんてできっこありません。

 そこで、Ellison, Lee and O’Rourke (2024) は、金本位制離脱のタイミングのズレに着目して、DiDを用いて、金本位制離脱と実質金利低下の因果関係（と思われるもの）を立証しました。 以下、ELO論文（これまでの悪行でバレているかもしれませんが、経済学者は頭文字を取らないと生きていけない質なのです）が用いたDiDの手法について述べます。

 DiDのアイディアは、「処置があった群についても、処置がなかったときの処置の前後での変化は、処置のなかった群のそれと同じはずだ」というものです。これを平行トレンドの仮定といいます。
 数式で書くのなら、E[ΔYᵢ(0)|Dᵢ=1]=E[ΔYᵢ(0)|Dᵢ=0]ということになります（Δは差分です）。これが満たされる限り、

DiD=E[ΔYᵢ(1)|Dᵢ=1]-E[ΔYᵢ(0)|Dᵢ=0]=E[ΔYᵢ(1)|Dᵢ=1]-E[ΔYᵢ(0)|Dᵢ=1]=E[Yᵢ(1)-Yᵢ(0)|Dᵢ=1]

が得られます（ただし、Yᵢ(1), Yᵢ(0)は処置後の値です）。
 したがって、DiDが正なら、Dという処置は、少なくともD=1の群について、平均的にはYを増加させるということがわかります。もちろん、負ならその逆に、Dという処置が、D=1の群について平均的にはYを減少させるということです。

 ELO論文の「処置」は、その国iが金本位制を早期に離脱した（D=1）か、遅くまで金本位制にとどまった（D=0）かです。そのもとで、早期離脱組が金本位制を離脱した時期の前後での、実質金利Yの変化を見ます。
 結果は以下の通りに表にまとめました。
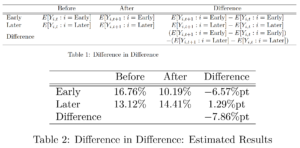（出所: ELO 2024, Table 4に基づいて筆者が作成）

 この結果は、もしも仮定が正しければ、金本位制の離脱は、少なくとも早期に金本位制を離脱した群において、実質金利を7.86%ポイント低下させたという因果関係を意味します。
 ようやく因果関係が得られました！　バンザイ・チャント重点！

 ……といきたいところですが、「仮定が正しければ」という留保を置いたように、私たちは重要な仮定、平行トレンドの仮定を確認する必要があります。
 もちろん、平行トレンドが本当に厳密に成り立っているのかは、やはり平行世界かタイムマシンを必要とするので、あくまでも「成立してるっぽいぞ」という程度の確認にとどまりますが。

 ひとつの重要なポイントは、事前のトレンドの動きです。もしも、事前のトレンドがD=1の群とD=0の群でまったく違う動きをしていたら、明らかに平行トレンドも成り立ちそうにありません。逆に、もしも事前のトレンドが平行であれば、特段の事情がない限りは、その後もおおむね平行だったんじゃないか？　という予想を立てることも、それほどおかしくはありません。「平行トレンドの仮定が成り立つ！」と断言することはできませんが、積極的に否定する理由はなかろうということです。
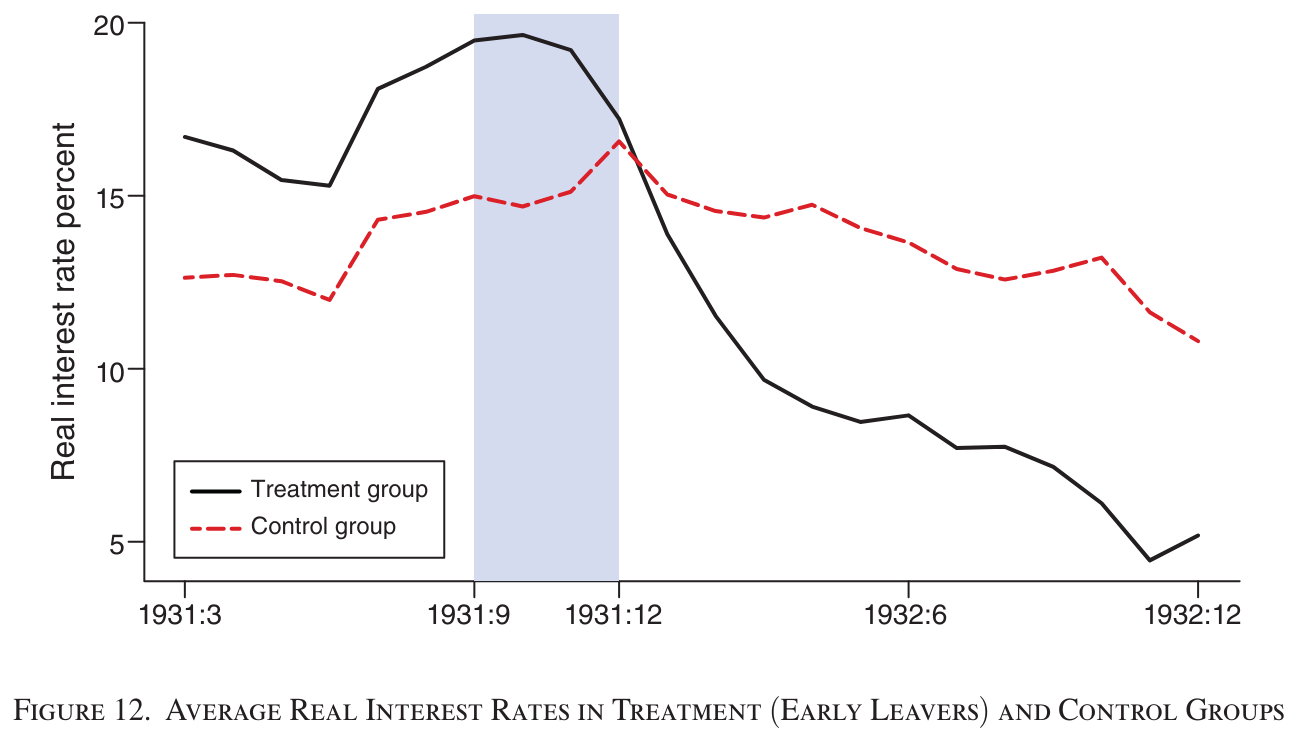
 実際、ELO論文での事前のトレンドは図の通りです。
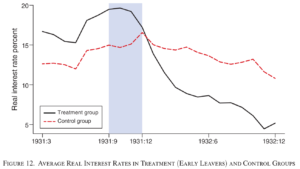（出典: ELO 2024, Figure 12）

 事前のトレンドはおおむね平行であり、色が塗られた時期に黒線（D=1の群）が金本位制を離脱したことで一気に実質金利が低下していますから、どうやら因果関係っぽいものがありそうだぞ、と言っても差し支えなさそうです。

おわりに

 お疲れ様でした。ここまで読んだ人が果たして何人いることやら……（え
 ともあれ、今回の記事で伝えたかったことは、「因果関係がある」と主張するのはめちゃくちゃ難しいんだぞ、ということです。その雰囲気だけでも伝わっていれば花丸百点満点だと思っています。

 ウカツに因果を主張するとニンジャが笑う。実際コワイので備えよう。

引用文献

Angrist, Joshua David. 1990. “Lifetime Earnings and the Vietnam Era Draft Lottery: Evidence from Social Security Administrative Records.” American Economic Review, 80 (3): 313–36.
Ellison, Martin, Sang Seok Lee, and Kevin Hjortshøj O’Rourke. 2024. “The Ends of 27 Big Depressions.” American Economic Review, 114 (1): 134–68.