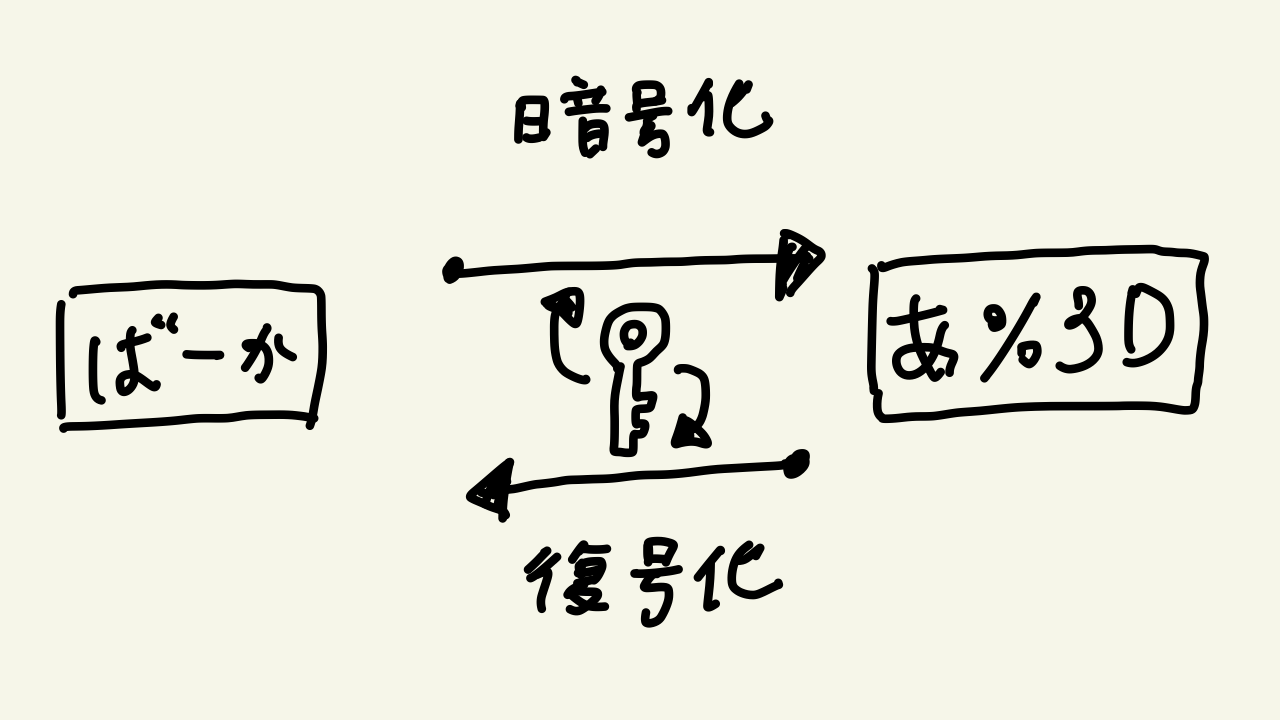
安全な暗号と共通鍵 まえがき 最近は冷え込みも激しく、椅子の上であぐらをかいて足の指先を温める季節となりました。そんな今日は12月中旬です。大学のレポートを書く時のように、「だ・である」調か「です・ます」調のどちらを選ぼうか悩んでいるところではございますが、早速本題に入りましょう。 前回書いたブログでは、シーザー暗号だとか単一換字式暗号だとかの話をしました。昔から使われている暗号化技術ではありましたが、無線やコンピュータが発明されるにあたって急速に陳腐化することになります。 安全な暗号 そもそも、安全な暗号とは何でしょう? この疑問に答えるためには、別にアマゾンの奥地に行く必要はありません。ネットの海を泳げば自ずと、「ケルクホフスの原理」にたどり着くでしょう。 ご推察の通り、「ケルクホフスの原理」はケルクホフスが1883年に発表したものです。この原理は6つの条件があり、特に下記の2番目のものが重要とされています。 ・「ケルクホフスの原理」 暗号化通信は以下を満たさねかればならない(何となくの意訳、正確なものはURLから) 1. 現実的に解読不能であること 2. 暗号化の方法は広く知られていても問題ないこと 3. 鍵は簡単に通信と保持ができ、容易に変更可能であること 4. 電信通信できること 5. 携帯可能で、一人で使えること 6. とっても楽で使いやすいこと 『Kerckhoffs’ principles – Cryptographie militaire』 https://www.petitcolas.net/kerckhoffs/ 前回説明したシーザー暗号は、暗号化方法がわからなければただの文字の羅列に見られるかもしれません。最初からシーザー暗号と知っていれば解読は容易ですが、知らなければちょっとした時間がかかるでしょう。けれども、「ケルクホフスの原理」は暗号化方法は知られていると思っておけ、と言っているのです。つまり、安全な暗号とは秘密の鍵さえ守ることができれば、解読されないもののことを言います。 共通鍵暗号 暗号通信の基本的な方法は、次のようになります。まず、送信者と受信者が通信の同意を行い、秘密の鍵を共有します。次に送信者が鍵を使用して暗号化を行い、安全でない経路を使用して暗号文を受信者へ送ります。最後に、受信者が受け取った暗号文に鍵を使用して復号することで、平文得ることができます。 このような暗号通信の方法を「共通鍵暗号化方式」と言ったりします。 DES DES(Data Encryption Standard)は、1977年にアメリカで標準化された「共通鍵暗号化方式」の暗号です。この暗号は標準化された当時は、解読不能とされていました。しかし、現在ではこの暗号化方式は使用されていません。コンピュータの進化が早すぎるせいで、さっくり鍵を見つけることができてしまうのです。現在主流の共通鍵暗号方式は、AESというものです。 今回はこのDESを試してみよう、と思ったりもしましたが、この暗号化方式はパソコン通信のために開発されたものです。つまり、ブログにひたすら0と1が並んでしまいます。世の中には、数式を見ただけで今日の夕食の献立を考えてしまう人がいるそうです。それと同様に、0と1が並ぶ世界を見せつけると、おそらく似たような人が現れるかもしれません(ちなみに、夕食にはコンソメを牛乳に溶かして作ったクリームシチューなんかが良いでしょう)。私が綺麗に説明し切れるかどうかという話は置いておくとして、今回は大まかに記述するにとどめます。 まず、鍵の長さは64bitです。64bitというのは、0か1のどちらかが64個並んでいると言うことです。エラー検出用の8bitを除くと実質的に鍵長は54bitとなります。この54bitの鍵を使って16個のサブ鍵を生成し、これを暗号化に使用します。… Continue reading 2-少しだけ難しい暗号を話してみる
Tag: 暗号
昔のかんたんな暗号を試してみる
暗号について 暗号と聞くと色々なことを思い浮かべることができる。例えば、現代社会のコンピュータを使った通信には暗号技術が使われている。これを破ることができれば、自分の銀行口座の預金額を5000兆円に書き換えることもできるかもしれない。また歴史関係で言えば、ドイツ国防軍が使用していたエニグマ暗号機は有名だ。しかし、例によってこのエニグマは連合国側によって解読されてしまっている。 暗号は送信者と受信者以外の第三者に情報が渡らないようにするための工夫である。しかし、暗号は常に解読される定めにある。どんなに巧妙な工夫を凝らして暗号化しても、解読者はあらゆる工夫を凝らして解読を試み、歴史上のあらゆる暗号は解読されてきた。現代でよく利用されている、非常に強固なRSA暗号ですら解読可能である。(具体的には、鍵長1024bitであれば現代の技術と莫大なリソースを割けばおそらく解読できるだろう、というもの) ここでは歴史上で昔から使われてきた暗号を実際に使ってみて、昔の人の気分を少しだけ感じてみようというものである。今回は分かりやすいように、アルファベット大文字を暗号文、アルファベット小文字を平文としている。また、ピリオドやコロン、空白文字などは無いものとして考える。 (暗号と復号の例文は十分注意を払って作成しているが、間違えているかもしれないのでご注意ください) シーザー暗号 シーザー暗号は、おそらく世界で一番有名で簡単な暗号である。暗号化の手順は、平文の文字を任意の数ずらすだけだ。復号化するときは、任意の数を鍵として暗号とは逆方向にずらせば良い。アルファベットを使用するとして任意の数を「3」とすれば、「a」という文字は「D」となり、「i」という文字は「L」となる。そして、「z」という文字は一周回って「C」になる。 例えば、鍵を「3」として「sekaishibeta」を暗号化すると、「VHNDLVKLEHWD」となる。パッとこの文字列を見せられると、意味のない文字列としか思えないが、「暗号化の手順」と「鍵」がわかっているのであれば復号できる。つまり、「シーザー暗号」という手順と「3」という鍵が渡されると、それぞれのアルファベットの3つ前を書き出せばいいことがわかる。最初の文字「V」は「s」と復号でき、「H」は「e」に対応する。 この暗号の問題点は第三者が暗号化手順を知っていた場合、すぐに解読されてしまうところにある。 ここに「TDWJRQJQNWCJR」という暗号文があったとする。もしあなたが「これはどうやらシーザー暗号で暗号化されている」と知っていた場合、どのくらいの時間で解読できるだろうか? アルファベットであれば文字の種類は26であるため、0文字ずらしたものから25文字ずらしたもの全てを書き出して意味を持ちそうな文章を見つけてしまえばいいのだ。つまり、総当たりで人間が解読できる程度には短い時間で可能である。この問題点を解決するために工夫したものが、次の暗号化の手順である。 (ちなみに、上記に書いた暗号文は重要機密であるため、ここで複合した文章は示さない。間違っても復号することのないように!) ちなみに、暗号化の手順が知られてしまうがゆえに脆弱なのであるから、その手順を秘密にしてしまえばいいのではないかと思った人もいると思う。しかし暗号界隈では、この手順を秘密にすることは機密性に全く関与しないことが指摘されている。その理由は、その手順が本当に安全であるかどうか検証ができないことにある。わざわざ自作するくらいなら、世界中の研究者が解読を試みて検証され続けてきた暗号化手順を使用した方がよっぽど安全である。 単一換字式暗号 単一換字式暗号は平文の文字と暗号文の文字が一対一に対応する暗号である。平文「a」が「C」であるなら、暗号文「C」は必ず「a」になる。つまり、シーザー暗号も単一換字式暗号の一種であるが、ここではシーザー暗号を少し改良したものをつかう。 シーザー暗号は暗号化のパターンが単純で、26種類しかなかったのが問題であった。そのため、第三者の解読者が総当たりを試みる場合、その試行回数をべらぼうに増やすことを考える。 今回は、アルファベットそれぞれに対応する文字をランダムに決めた表を作成し、その表に従って暗号化と復号化を行うこととした。この場合、「a」に対応する文字を「D」と決めても、必ず「b」は「E」になるわけではなく、D以外の文字のどれかということになる(「a」に対応する文字が「D」であることがわかってるため)。もちろん、たまたま「b」が「E」に対応することもあるだろう。 これも実際に試してみよう。「sekaishibeta」を下記の表を鍵として暗号化すると「PQMFUPIUNQGF」となる。当然復号した文は、この表を見ながら文章を作っていけば良い。 さて、前提として第三者は暗号化手順はわかっているが鍵である対応表は持っていない。手順だけ分かっている解読者が、この暗号を解読するために総当たりで検証すると一体どれほどの時間がかかるか? シーザー暗号はずらすことしかしていないため26パターンであった。しかし、今回の方法は全部で26の階乗パターン存在する。つまり、最大「26 x 25 x 24 x … x 2… Continue reading 昔のかんたんな暗号を試してみる